How to determine the cross-section of a wire by diameter and vice versa: ready-made tables and calculation formulas

Wires are widely used in the field of electrical networks for various purposes.At first glance, energy transportation through cables and wires seems simple and understandable.

However, to ensure safe operation of electrical wiring, it is necessary to take into account a number of important nuances when designing and arranging electrical networks. One of these details is the ability to correctly calculate the cross-section of a wire by diameter, because the limit of the permissible current flowing through the conductor depends on the accuracy of the determination.

How to determine the cross-section or diameter, is there a difference between these parameters? Let's try to figure it out in the article. In addition, we have prepared summary tables that will help you choose a conductor depending on the installation conditions of the electrical network, the material of the cable core and the power characteristics of the connected units.

Necessity and procedure for calculation

Electric current powers a wide variety of equipment with varying power levels. And the power range is very wide.

Each individual electrical device represents a load, depending on the magnitude of which a current supply of a certain strength is required.

By “default” or simple ignorance of the basics of electrical engineering, it is easy to connect conductors, ignoring all existing requirements for diameters and cross-sections. Another question is what can come out of this practice during operation.

The required amount of current for the required load can be passed through wires of different diameters (sections).

But when the cross-section of the conductor is insufficient to pass a given amount of current, the effect of increased resistance occurs. As a result, heating of the wire (cable) is noted.

If you ignore this phenomenon and continue to pass current, there is a real danger of heating up to the point of fire. This situation threatens a serious emergency. That is why increased attention must be paid to calculations and selection of current transmission circuits to the load.

The consequences of inaccurate calculations of electrical conductors by cross-section (diameter) can be accompanied by phenomena ranging from minor deformation of the insulating material to a real fire and a major fire

Correct calculation, competent selection cables and wires has a positive effect on the operation of equipment acting as a load.

So, in addition to the safety factor, calculating the cross-sections of the electrical cable by diameter or vice versa is a mandatory action from the point of view of ensuring the efficient operation of electrical machines.

Determining the diameter of the conductor core

Actually, this operation can be performed with a simple linear measurement. For accurate measurements, it is recommended to use a point tool, such as a caliper, or even better, a micrometer.

A relatively low accuracy result, but quite acceptable for many applications of wires, is obtained by measuring the diameter with a regular ruler.

Measuring and determining the diameter of the core using a point tool, which is a caliper. This method of linear measurement gives a result that is sufficiently accurate for subsequent calculation of the conductor cross-section

Of course, the measurement should be carried out in the state of a bare conductor, that is, before the insulating covering is removed.

By the way, the insulating coating of, for example, a copper wire is also considered to be a thin layer of sprayed varnish, which also needs to be removed when a very precise calculation is required.

There is a “household” method of measuring diameter, suitable in cases where point measuring instruments are not available. To use this method, you will need an electrician's screwdriver and a school ruler.

The conductor for measurement is first stripped of insulation, after which it is wound tightly turn to turn on the screwdriver rod. Usually ten turns are wound - a convenient number for mathematical calculations.

Linear diameter measurement is another widely used method for determining a conductor parameter for calculating power (throughput). It is used using a regular ruler and any base where it is permissible to wind a conductor (+)

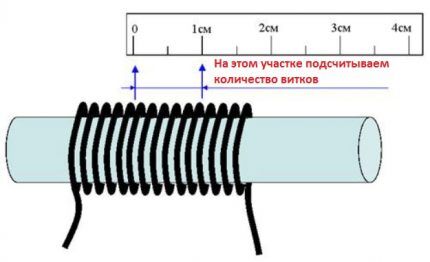
Next, the coil wound on the screwdriver rod is measured with a ruler from the first to the last turn. The resulting value on the ruler must be divided by the number of turns (in this case, 6). The result of this simple calculation will be the diameter of the wire core.

Calculating the cross-section of an electrical wire

To determine the cross-sectional value of the conductor core, you will have to use a mathematical formulation.

Essentially, the cross-section of a conductor core is the cross-sectional area - that is, the area of ​​a circle. The diameter of which is determined by the method described above.

The cross-section of the core is actually the area of ​​a circle.Accordingly, the calculation of this segment of geometric mathematics can be performed using the traditional formula, provided that the diameter or radius is known

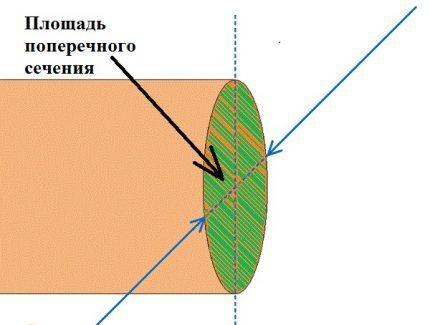
Based on the diameter value, it is easy to obtain the radius value by dividing the diameter in half.

Actually, you will need to add the constant “π” (3.14) to the obtained data, after which you can calculate the value of the cross section using one of the formulas:

S = π*R² or S = π/4*D²,

Where:

• D — diameter;
• R — radius;
• S - cross section;
• π is a constant corresponding to 3.14.

These classical formulas are also used to determine the cross-section of stranded conductors. The calculation strategy remains virtually unchanged, with the exception of some details.

In particular, the cross-section of one core from a bundle is initially calculated, after which the resulting result is multiplied by the total number of cores.

It is possible to calculate the cross-section of a stranded conductor using the same mathematical method that is applied to a single wire, but the number of existing conductors is additionally taken into account as a multiplier

Why should it be considered an important factor? section definition? An obvious point related directly to the Joule-Lenz law is because the cross-sectional parameter of the conductor determines the limit of the permissible current flowing through this conductor.

Determination of diameter by section

By mathematical calculation it is possible to determine the diameter of the conductor core when the cross-sectional parameter is known.

This, of course, is not the most practical option, given the availability of simpler ways to determine the diameter, but the use of this option is not excluded.

Measuring the diameter with high accuracy using a metalworking tool - a micrometer, gives almost the same result when calculations are carried out using the formula

To perform the calculation, you will need virtually the same numerical information that was used when calculating the cross section using a mathematical formula.

That is, the constant “π” and the value of the area of ​​the circle (section).

Applying these formula values ​​below gives the diameter value:

D = √4S/π,

Where:

• D — diameter;
• S - cross section;
• π is a constant corresponding to 3.14.

The use of this formula may be relevant when the section parameter is known and there are no suitable tools at hand to measure the diameter.

The cross-section parameter can be obtained, for example, from the documentation for the conductor or from the calculation table, which presents the most commonly used classic options.

Tables for selecting a suitable conductor

A convenient and practical option for selecting the desired wire (cable) is to use special tables that indicate the diameters and cross-sections relative to the power and/or currents carried.

Having such a table at hand is an easy and simple way to quickly determine the conductor for the required electrical installation.

Determining the required values ​​using a classic table is one of the most convenient ways to select the required conductor during installation work

Considering that traditional conductors for electrical installations are products with copper or aluminum conductors, there are tables for both types of metals.

Also, tabular data often presents values ​​for voltages of 220 volts and 380 volts.Plus, the installation conditions are taken into account - closed or open wiring.

In fact, it turns out that one sheet of paper or a picture loaded into a smartphone contains voluminous technical information that allows you to do without the above-mentioned mathematical (linear) calculations.

Moreover, many manufacturers of cable products, in order to make it easier for the buyer to choose the right conductor, for example, for installing sockets, offer a table in which all the necessary values ​​are entered.

All that remains is to determine what load is planned for a specific electrical point and how the installation will be performed, and based on this information, select the correct wire with copper or aluminum conductors.

Examples of such options for calculating the cross-sectional diameter of a wire are given in the table, which discusses options for copper and aluminum conductors, as well as methods for laying wiring - open or hidden type. From the first table you can determine the indicator power and current cross sections.

Table of cross-sectional diameters of copper and aluminum conductors depending on installation conditions

In addition, there is a standard for cross-sections and diameters that applies to round (shaped) unsealed and sealed conductive conductors of cables, wires, and cords. These parameters are regulated GOST 22483-2012.

The standard covers cables made of copper (tinned copper), aluminum wire without metal coating or with metal coating.

Copper and aluminum conductors of cables and wires for stationary installation are divided into classes 1 and 2. Wires, cords, cables for non-stationary and stationary installation, where an increased degree of flexibility in installation is required, are divided into classes from 3 to 6.

Conformity table by class for cable (wire) copper conductors

For aluminum conductors and cables, GOST 22483-2012 also provides parameters for the nominal cross-section of the core, which correspond to the corresponding diameter, depending on the class of the core.

Moreover, according to the same GOST, the indicated diameters can be used for class 1 copper conductor if you need to calculate its minimum diameter.

Conformity table by class for cable (wire) aluminum conductors

Additional recommendations for choosing the type of wires and cables for arranging electrical networks in an apartment and house are given in the articles:

1. Which wire to use for wiring in the house: recommendations for choosing
2. Which cable to use for wiring in a wooden house: types of non-flammable cable and its safe installation
3. Which cable to use for wiring in an apartment: overview of wires and choosing the best option

Conclusions and useful video on the topic

The video below demonstrates a practical example of determining the cross-section of a conductor using simple methods.

Watching the video is recommended, as the clearly presented information helps to increase the amount of knowledge:

Working with electrical wires always requires a responsible attitude from a calculation point of view.

Therefore, an electrician of any rank must know the calculation methodology and be able to use existing technical tables. This achieves not only significant savings on installation costs due to accurate calculations, but most importantly, the safety of operation of the introduced line is guaranteed.

Do you have anything to add or have questions about determining the wire cross-section? You can leave comments on the publication, participate in discussions and share your own experience in selecting wires for installing an electrical network in a house or apartment. The contact form is located in the lower block.