Calculation of heating radiators: how to calculate the required number and power of batteries
A well-designed heating system will provide housing with the required temperature and all rooms will be comfortable in any weather.But in order to transfer heat to the air space of residential premises, you need to know the required number of batteries, right?
Calculation of heating radiators, based on calculations of the thermal power required from the installed heating devices, will help to find out this.
Have you never done such calculations and are afraid of making mistakes? We will help you understand the formulas - the article discusses a detailed calculation algorithm and analyzes the values of individual coefficients used in the calculation process.
To make it easier for you to understand the intricacies of the calculation, we have selected thematic photographic materials and useful videos that explain the principle of calculating the power of heating devices.
The content of the article:
- Simplified calculation of heat loss compensation
- Detailed formula for calculating thermal power
- Orientation of rooms according to cardinal directions
- Taking into account the influence of external walls
- Dependence of radiators on thermal insulation
- Climate is an important factor in arithmetic
- Features of calculation of high rooms
- Design role of ceiling and floor
- The quality of the frames is the key to warmth
- Window size matters
- Impact of closed battery
- Radiator connection efficiency
- Practical example of calculating thermal power
- Specific thermal power of battery sections
- Calculation of the number of radiator sections
- Increased heat transfer efficiency
- Conclusions and useful video on the topic
Simplified calculation of heat loss compensation
Any calculations are based on certain principles. The calculations of the required thermal power of batteries are based on the understanding that well-functioning heating devices must fully compensate for the heat losses that occur during their operation due to the characteristics of the heated premises.
For living rooms located in a well-insulated house, located, in turn, in a temperate climate zone, in some cases a simplified calculation of compensation for heat leakage is suitable.
For such premises, calculations are based on a standard power of 41 W required to heat 1 cubic meter. living space.
The formula for determining the thermal power of radiators necessary to maintain optimal living conditions in a room is as follows:
Q = 41 x V,
Where V – volume of the heated room in cubic meters.
The resulting four-digit result can be expressed in kilowatts, reducing it at the rate of 1 kW = 1000 W.
Detailed formula for calculating thermal power
When making detailed calculations of the number and size of heating radiators, it is customary to start from the relative power of 100 W required for normal heating of 1 m² of a certain standard room.
The formula for determining the thermal power required from heating devices is as follows:
Q = ( 100 x S ) x R x K x U x T x H x W x G x X x Y x Z
Factor S in calculations, nothing more than the area of the heated room, expressed in square meters.
The remaining letters are various correction factors, without which the calculation will be limited.

But even additional design parameters cannot always reflect all the specifics of a particular room. When in doubt about calculations, it is recommended to give preference to indicators with large values.
It is easier to then reduce the temperature of the radiators using temperature control devicesthan to freeze when their thermal power is insufficient.
Next, each of the coefficients involved in the formula for calculating the thermal power of batteries is discussed in detail.
At the end of the article, information is given on the characteristics of collapsible radiators made of different materials, and the procedure for calculating the required number of sections and the batteries themselves is discussed based on the basic calculation.
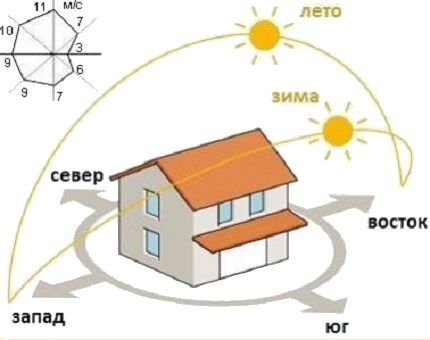
Orientation of rooms according to cardinal directions
And on the coldest days, the energy of the sun still affects the thermal balance inside the home.
The “R” coefficient of the formula for calculating thermal power depends on the orientation of the rooms in one direction or another.
- Room with a window to the south - R = 1.0. During daylight hours, it will receive maximum additional external heat compared to other rooms. This orientation is taken as the basic one, and the additional parameter in this case is minimal.
- Window faces west - R = 1.0 or R = 1.05 (for areas with short winter days). This room will also have time to receive its portion of sunlight. Although the sun will look there in the late afternoon, the location of such a room is still more favorable than the eastern and northern ones.
- The room is oriented to the east - R = 1.1. The rising winter luminary is unlikely to have time to properly heat such a room from the outside. Battery power will require additional watts. Accordingly, we add a significant amendment of 10% to the calculation.
- Outside the window there is only north - R = 1.1 or R = 1.15 (a resident of northern latitudes will not be mistaken if he takes an additional 15%). In winter, such a room does not see direct sunlight at all. Therefore, it is recommended to adjust the calculations of the heat output required from radiators by 10% upward.
If winds of a certain direction prevail in the area where you live, it is advisable for rooms with windward sides to increase R by up to 20% depending on the strength of the blow (x1.1÷1.2), and for rooms with walls parallel to cold currents, raise the value of R by 10% (x1.1).
Taking into account the influence of external walls
In addition to the wall with a window or windows built into it, other walls of the room may also have contact with the cold outside.
The external walls of the room determine the coefficient “K” of the calculation formula for the thermal power of radiators:
- The presence of one street wall near a room is a typical case. Here everything is simple with the coefficient - K = 1.0.
- Two external walls will require 20% more heat to heat the room - K = 1.2.
- Each subsequent external wall adds 10% of the required heat transfer to the calculations. For three street walls - K = 1.3.
- The presence of four external walls in a room also adds 10% - K = 1.4.
Depending on the characteristics of the room for which the calculation is being performed, the appropriate coefficient must be taken.
Dependence of radiators on thermal insulation
Properly and reliably insulated housing from the winter cold allows you to reduce the budget for heating the interior space, and significantly.
The degree of insulation of street walls is subject to the “U” coefficient, which reduces or increases the calculated thermal power of heating devices:
- U=1.0 - for standard external walls.
- U = 0.85 - if the insulation of street walls was carried out according to a special calculation.
- U = 1.27 - if the external walls are not cold-resistant enough.
Walls made of climate-appropriate materials and thickness are considered standard. And also of reduced thickness, but with a plastered outer surface or with a surface external thermal insulation.
If the area of the room allows, then you can make insulation of walls from the inside. And there is always a way to protect walls from the cold outside.

Climate is an important factor in arithmetic
Different climate zones have different minimum outdoor temperatures.
When calculating the heat transfer power of radiators, a coefficient “T” is provided to take into account temperature differences.
Let's consider the values of this coefficient for various climatic conditions:
- T=1.0 up to -20 °C.
- T=0.9 for winters with frost down to -15 °C
- T=0.7 – down to -10 °C.
- T=1.1 for frosts down to -25 °C,
- T=1.3 – up to -35 °C,
- T=1.5 – below -35 °C.
As we can see from the list above, winter weather down to -20 °C is considered normal. For areas with such the least cold, a value of 1 is taken.
For warmer regions, this calculation factor will lower the overall calculation result. But for areas of harsh climates, the amount of heat energy required from heating devices will increase.
Features of calculation of high rooms
It is clear that of two rooms with the same area, the one with the higher ceiling will need more heat. The coefficient “H” helps to take into account the correction for the volume of heated space in calculating thermal power.
At the beginning of the article, it was mentioned about a certain regulatory premises. This is considered to be a room with a ceiling of 2.7 meters or lower. For it, take a coefficient value equal to 1.
Let's consider the dependence of the coefficient H on the height of the ceilings:
- H=1.0 - for ceilings 2.7 meters high.
- H=1.05 - for rooms up to 3 meters high.
- H = 1.1 - for a room with a ceiling up to 3.5 meters.
- H = 1.15 – up to 4 meters.
- H = 1.2 - heat requirement for a higher room.
As you can see, for rooms with high ceilings, 5% should be added to the calculation for every half meter of height, starting from 3.5 m.
According to the law of nature, warm heated air rushes upward. To mix its entire volume, heating devices will have to work hard.

Design role of ceiling and floor
Reducing the thermal power of batteries is not only good insulated external walls. The ceiling in contact with the warm room also allows you to minimize losses when heating the room.
The coefficient “W” in the calculation formula is precisely to provide for this:
- W=1.0 - if there is, for example, an unheated, uninsulated attic upstairs.
- W=0.9 - for an unheated but insulated attic or other insulated room above.
- W=0.8 - if the room on the floor above is heated.
The W indicator can be adjusted upward for rooms on the first floor if they are located on the ground, above an unheated basement or basement space. Then the numbers will be as follows: the floor is insulated +20% (x1.2); the floor is not insulated +40% (x1.4).
The quality of the frames is the key to warmth
Windows were once a weak point in the thermal insulation of a living space. Modern frames with double-glazed windows have significantly improved the protection of rooms from the street cold.
The degree of window quality in the formula for calculating thermal power is described by the coefficient “G”.
The calculation is based on a standard frame with a single-chamber double-glazed window, whose coefficient is equal to 1.
Let's consider other options for using the coefficient:
- G=1.0 - frame with single-chamber double-glazed windows.
- G=0.85 - if the frame is equipped with a two- or three-chamber double-glazed window.
- G = 1.27 - if the window has an old wooden frame.
So, if the house has old frames, then the heat loss will be significant. Therefore, more powerful batteries will be required. Ideally, it is advisable to replace such frames, because these are additional heating costs.
Window size matters
Following logic, it can be argued that the greater the number of windows in the room and the wider their view, the more sensitive the heat leakage through them. The "X" factor in the formula for calculating the thermal power required from batteries reflects this.

The norm is the result of dividing the area of window openings by the area of the room equal to 0.2 to 0.3.
Here are the main values of the X coefficient for various situations:
- X = 1.0 - at a ratio from 0.2 to 0.3.
- X = 0.9 - for area ratio from 0.1 to 0.2.
- X = 0.8 - with a ratio of up to 0.1.
- X = 1.1 - if the area ratio is from 0.3 to 0.4.
- X = 1.2 - when it is from 0.4 to 0.5.
If the footage of window openings (for example, in rooms with panoramic windows) goes beyond the proposed ratios, it is reasonable to add another 10% to the X value when the area ratio increases by 0.1.
The door in the room, which is regularly used in winter to access an open balcony or loggia, makes its own adjustments to the heat balance.For such a room, it would be correct to increase X by another 30% (x1.3).
Thermal energy losses can be easily compensated by compact installation of a ducted water or electric convector under the balcony entrance.
Impact of closed battery
Of course, the radiator that is less surrounded by various artificial and natural obstacles will give off heat better. In this case, the formula for calculating its thermal power has been expanded due to the “Y” coefficient, which takes into account the operating conditions of the battery.
The most common location for heating devices is under the windowsill. In this position, the coefficient value is 1.
Let's consider typical situations for placing radiators:
- Y=1.0 - right under the windowsill.
- Y = 0.9 - if the battery suddenly turns out to be completely open on all sides.
- Y = 1.07 - when the radiator is obscured by a horizontal projection of the wall
- Y = 1.12 - if the battery located under the window sill is covered with a front casing.
- Y=1.2 - when the heating device is blocked from all sides.
Long blackout curtains pulled down also cause the room to become colder.

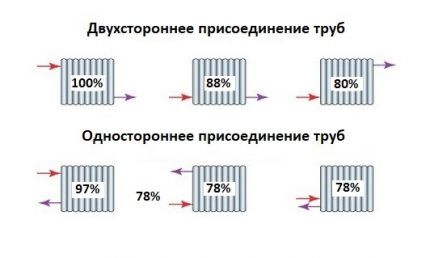
Radiator connection efficiency
The efficiency of its operation directly depends on the method of connecting the radiator to the indoor heating wiring. Homeowners often sacrifice this indicator for the sake of the beauty of the room. The formula for calculating the required thermal power takes all this into account through the “Z” coefficient.
Here are the values of this indicator for various situations:
- Z=1.0 - connecting the radiator to the general circuit of the heating system using a “diagonal” method, which is the most justified.
- Z = 1.03 - another, most common due to the short length of the liner, is the option of connecting “from the side”.
- Z = 1.13 - the third method is “from below on both sides”. Thanks to plastic pipes, it quickly took root in new construction, despite its much lower efficiency.
- Z = 1.28 - another, very ineffective “from below on one side” method. It deserves consideration only because some radiator designs are equipped with ready-made units with both supply and return pipes connected to one point.
The air vents installed in them will help to increase the efficiency of heating devices, which will promptly save the system from “airing”.
The operating principle of any water heating device is based on the physical properties of hot liquid to rise upward and, after cooling, to move downward.
Therefore, it is strongly recommended not to use heating system connections to radiators in which the supply pipe is at the bottom and the return pipe is at the top.
Practical example of calculating thermal power
Initial data:
- A corner room without a balcony on the second floor of a two-story cinder block plastered house in a windless region of Western Siberia.
- Room length 5.30 m X width 4.30 m = area 22.79 sq.m.
- Window width 1.30 m X height 1.70 m = area 2.21 sq.m.
- Room height = 2.95 m.
Calculation sequence:
| Room area in sq.m.: | S = 22.79 |
| Window orientation – south: | R = 1.0 |
| Number of external walls – two: | K = 1.2 |
| Insulation of external walls is standard: | U=1.0 |
| Minimum temperature – up to -35°C: | T=1.3 |
| Room height – up to 3 m: | H=1.05 |
| The upstairs room is an uninsulated attic: | W=1.0 |
| Frames – single-chamber double-glazed windows: | G=1.0 |
| The ratio of window and room areas is up to 0.1: | X = 0.8 |
| Radiator position – under the window sill: | Y=1.0 |
| Radiator connection – diagonally: | Z=1.0 |
| Total (remember to multiply by 100): | Q = 2,986 Watts |
Below is a description of calculating the number of radiator sections and the required number of batteries. It is based on the obtained results of thermal power, taking into account the dimensions of the proposed installation locations of heating devices.
Regardless of the results, it is recommended to equip not only window sill niches with radiators in corner rooms. Batteries should be installed near “blind” external walls or near corners that are subject to the greatest freezing under the influence of street cold.
Specific thermal power of battery sections
Even before performing a general calculation of the required heat transfer of heating devices, it is necessary to decide what material the collapsible batteries will be installed in the premises from.
The choice should be based on the characteristics of the heating system (internal pressure, coolant temperature). At the same time, do not forget about the greatly varying costs of purchased products.
How to correctly calculate the required number of different batteries for heating will be discussed further.
At a coolant temperature of 70 °C, standard 500 mm sections of radiators made of dissimilar materials have unequal specific thermal power “q”.
- Cast iron - q = 160 Watt (specific power of one cast iron section). Radiators from this metal suitable for any heating system.
- Steel - q = 85 Watt. Steel tubular radiators can work in the harshest operating conditions. Their sections are beautiful in their metallic shine, but have the lowest heat output.
- Aluminum - q = 200 Watt. Lightweight, aesthetic aluminum radiators should be installed only in autonomous heating systems in which the pressure is less than 7 atmospheres. But their sections have no equal in terms of heat transfer.
- Bimetal - q = 180 Watt. Entrails bimetallic radiators made of steel, and the heat-dissipating surface is made of aluminum. These batteries will withstand all pressure and temperature conditions. The specific thermal power of bimetal sections is also high.
The given values of q are rather arbitrary and are used for preliminary calculations. More accurate figures are contained in the passports of the purchased heating devices.
Calculation of the number of radiator sections
Collapsible radiators made of any material are good because to achieve their calculated thermal power, you can add or subtract individual sections.
To determine the required number “N” of battery sections from the selected material, the formula is followed:
N=Q/q,
Where:
- Q = previously calculated required thermal power of devices for heating the room,
- q = specific thermal power of a separate section of batteries proposed for installation.
Having calculated the total required number of radiator sections in the room, you need to understand how many batteries need to be installed. This calculation is based on a comparison of the dimensions of the proposed locations installation of heating devices and battery sizes taking into account the connections.

For preliminary calculations, you can arm yourself with data on the width of sections of different radiators:
- cast iron = 93 mm,
- aluminum = 80 mm,
- bimetallic = 82 mm.
When making collapsible radiators from steel pipes, manufacturers do not adhere to certain standards. If you want to install such batteries, you should approach the issue individually.
You can also use our free online calculator to calculate the number of sections:
Increased heat transfer efficiency
When the radiator heats the internal air of the room, intense heating of the external wall in the area behind the radiator also occurs.This leads to additional unjustified heat losses.
To increase the efficiency of heat transfer from the radiator, it is proposed to fence off the heating device from the outer wall with a heat-reflecting screen.
The market offers many modern insulating materials with a heat-reflecting foil surface. The foil protects the warm air heated by the battery from contact with the cold wall and directs it inside the room.
For proper operation, the boundaries of the installed reflector must exceed the dimensions of the radiator and protrude 2-3 cm on each side. The gap between the heating device and the thermal protection surface should be left 3-5 cm.
To make a heat-reflecting screen, we can recommend isospan, penofol, alufom. A rectangle of the required dimensions is cut out from the purchased roll and fixed on the wall at the location where the radiator is installed.
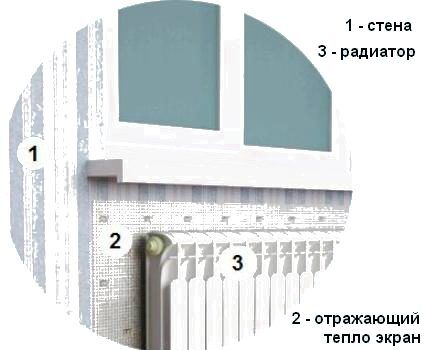
It is recommended to separate the insulation sheet from the external wall with a small air gap, for example, using a thin plastic grid.
If the reflector is joined from several parts of insulating material, the joints on the foil side must be sealed with metallized adhesive tape.
Conclusions and useful video on the topic
Short films will present the practical implementation of some engineering tips in everyday life. In the following video you can see a practical example of calculating heating radiators:
Changing the number of radiator sections is discussed in this video:
The following video will tell you how to mount the reflector under the battery:
The acquired skills of calculating the thermal power of different types of heating radiators will help the home craftsman in the competent design of the heating system. And housewives will be able to check the correctness of the battery installation process by third-party specialists.
Have you independently calculated the power of heating batteries for your home? Or have you encountered problems resulting from the installation of low-power heating devices? Tell our readers about your experience - please leave comments below.




In one of the rooms in our apartment, the builders clearly miscalculated - the window is 2.1 m long, and the radiator is 80 cm, and it starts earlier, i.e. reaches approximately the middle of the first valve. Accordingly, it is almost always cold on the opposite side of the window, especially when there is wind or frost. The heat insulation screen helps quite well, but we will still do additional external insulation in the spring.
All my life I lived in houses and apartments with cast iron radiators. They were always as wide as a window, I’m so used to it. I recently replaced old batteries with modern devices, and they were small, half the size of a window, and they also assured me that this would be enough for heating. Of course, the room is cold, the radiator can’t cope. I'll change everything in the spring. How much easier it was with cast iron radiators(
Hello. Thanks for the detailed information.The formula you provided for calculating thermal power includes heating the room to what temperature? That is, the coefficients of this formula as a result only allow you to find out about heat loss in kilowatts, or does the formula (coefficients) include a reserve that will compensate for heat loss and plus ensure heating of the room temperature to a specific degree?